Lab 12: Inverted Pendulum Control – MAE 4190 Fast Robots

In Lab 12, I embraced the open-endedness of our last assignment and worked on the challenge of turning the car into an inverted pendulum.

Before I get into the details of my pendulum experiments, I want to quickly outline what I would have done had I completed Lab 12 as written, so as to convey my understanding of the task. Broadly, I would have chosen local path planning and used a combination of Lab 11's localization routine and the PID controllers from Lab 5 and Lab 6 to navigate between waypoints in the arena. Put simply, I have spent a lot of time on developing those systems this semester and would have wanted to bring everything together for this lab. I would have additionally used the ToF sensors to avoid hitting the walls in the event of inaccurate localization, and orientation PID control to set headings for each next waypoint. I would also have used the IMU's DMP features to reliably track my orientation throughout the navigation process, thereby giving me at least some sense of the global state of the car in relation to the map.

I predict that I would have experienced challenges with accurate distance measurements while moving from point to point using linear PID control, because the ToF sensors would have underperformed when attempting to gather readings at odd angles. For example, when moving from waypoint #1 to #2, pulses sent by both my front and rear ToF sensors would have met the walls at roughly 45 degrees of incidence. Those pulses would likely have bounced away from the car and not yielded terribly accurate estimates of the distances to the walls, so it's highly probably that my car would have had trouble finding waypoint #2 on a first attempt. It would then have needed to localize part-way between the points and adjust accordingly. I predict I would have faced a similar issue between waypoints #3 and #4.

An Alternate Objective

In preparation for ECE Robotics Day on May 7th, I had been playing around with some additional ideas for stunts because I wasn't completely satisfied with the drift I managed in Lab 8. One idea was to have the car do donuts on the floor of Duffield Atrium—"donuts" in this case being loosely defined as a circular drift maneuver sustained over a few seconds.

While working on the donut business, my friend and classmate Leo Dombrovski was simultaneously trying to get inverted pendulum control working on his car. The morning of Robotics Day, Leo showed off the beginnings of a working solution, which inspired me to pursue the same challenge.

After some time tinkering with the basic premise—PID control on the pitch of the robot—I had a rough proof-of-concept running. The car could stand upright on its back wheels for a couple of seconds before falling over.

At this point, both Leo and I had drawn some attention from the crowd. Jonathan Jaramillo, our instructor, and Prof. Peterson, who designed the class some years ago, were excited to see students tackle the classic dynamics problem on Fast Robots hardware.

By the end of Robotics Day, I had spent some five hours in Duffield, working first on my donut stunt and then the inverted pendulum problem. In recognition of our efforts, Jonathan offered Leo and me the option to write about the pendulum challenge for Lab 12 instead of the original waypoint navigation tasks. So here I am, doing just that.

Implementation

As I hinted previously, the crux of the inverted pendulum problem is a PID controller on the pitch of the car. Because of the way I had mounted my IMU earlier in the semester, an upright orientation of the robot on its rear wheels constituted a pitch measurement of 90 degrees. No matter, I thought, I could just subtract 90 from any given reading and get an error relative to a set point of 0 degrees—straight up. Unsurprisingly, it wasn't that easy.

As with all my IMU shenanigans lately, I used the DMP chip to get more accurate pitch readings. This required a small addition to the quaternion-Euler conversions I first described in Lab 6.

 // Convert to double, scale to +/- 1 by dividing by 2^30
 double qx = dmp.Quat6.Data.Q1 / 1073741824.0;
 double qy = dmp.Quat6.Data.Q2 / 1073741824.0;
 double qz = dmp.Quat6.Data.Q3 / 1073741824.0;

 double qw = sqrt(1.0 - min(((qx * qx) + (qy * qy) + (qz * qz)), 1.0));

!// Pitch (y-axis rotation)
!double sinp = 2.0 * (qw * qy - qx * qz);
!double pitch = asin(sinp) * 180.0 / PI - 90.0;

 // Yaw (z-axis rotation)
 double siny = 2.0 * (q0 * qz + qx * qy);
 double cosy = 1.0 - 2.0 * (qy * qy + qz * qz);
 double yaw = atan2(siny, cosy) * 180.0 / PI;

Reading pitch and subtracting 90 degrees worked, in principle. Standing the car straight up yielded pitch readings of 0 degrees, just like I had wanted.

But there was a problem. The pitches on both sides of perfectly vertical were positive angles between 0 and 90, meaning there was no sense of direction. For PID control to work on pitch, I needed the slight rotations fore and aft of the desired vertical orientation to register as positive and negative angles, respectively. Leo gave me a good suggestion for how to adjust the math to achieve this, which I implemented in my own terms below.

// Pitch (y-axis rotation)
double sinp = 2.0 * (qw * qy - qx * qz);
double cosy = 1.0 - 2.0 * (qy * qy + qz * qz);
double pitch = atan2(sinp, cosy) * 180.0 / PI + 90.0;

The idea here is to take the $\arctan$ of the quaternion components to represent rotation about the $y$ axis in the car's frame, rather than the $\arcsin$ operation I had used before. Normally, doing this sort of thing in robotics comes with a caveat: gimbal lock at the poles. However, because my car's orientation is not directly controlled by 3D actuators and because gravity will happily resolve any singularity when pointing straight up, that was of no concern to me here.

With the pitch now measured with each cycle of the main control loop, I added an inverted pendulum PID controller to the Artemis, complete with filtering on the D term and a safety switch to stop the car if the pitch to either side of vertical exceeded 15 degrees, at which point the car was doomed to fall.

#define PITCH_SAFETY 15 // degrees

void pidPenControl() {
    last_pid_time = current_pid_time;
    current_pid_time = micros() / 1.e6; // secs
    pid_dt = current_pid_time - last_pid_time;

    last_error = current_error;
    current_error = current_pitch_reading - pid_pen_target;

    P_term = Kp_pen * current_error;

    error_integral = constrain(error_integral + current_error * pid_dt, -INTEGRAL_THRESHOLD, INTEGRAL_THRESHOLD);
    I_term = Ki_pen * error_integral;

    D_term = Kd_pen * (current_error - last_error) / pid_dt;

    last_filtered_D_term = filtered_D_term;
    filtered_D_term = D_LPF_ALPHA * D_term + (1-D_LPF_ALPHA) * last_filtered_D_term;

    speed = 0.01 * (P_term + I_term + filtered_D_term);

    if (!flag_enable_motors) return;

    // Stop motors if the car is tilted too far or the speed is insufficient
    if (abs(current_error) > PITCH_SAFETY || abs(speed) < pid_pen_threshold) {
        idleMotors();
        return;
    }

    driveMotors(speed, speed);
}

The gains I had landed on during Robotics Day were a $K_{p}$ of 2.7 and a $K_{d}$ of -0.4. I ended up zeroing out the $K_{i}$ term because it didn't seem to help in any significant way, ultimately leaving me with a PD controller. The video below shows this in action.

I then spent some additional time tuning the gains and the motor control to improve the car's stability. My final gains were a $K_{p}$ of 2.4 and a $K_{d}$ of -0.3. The video and plot below show the results.

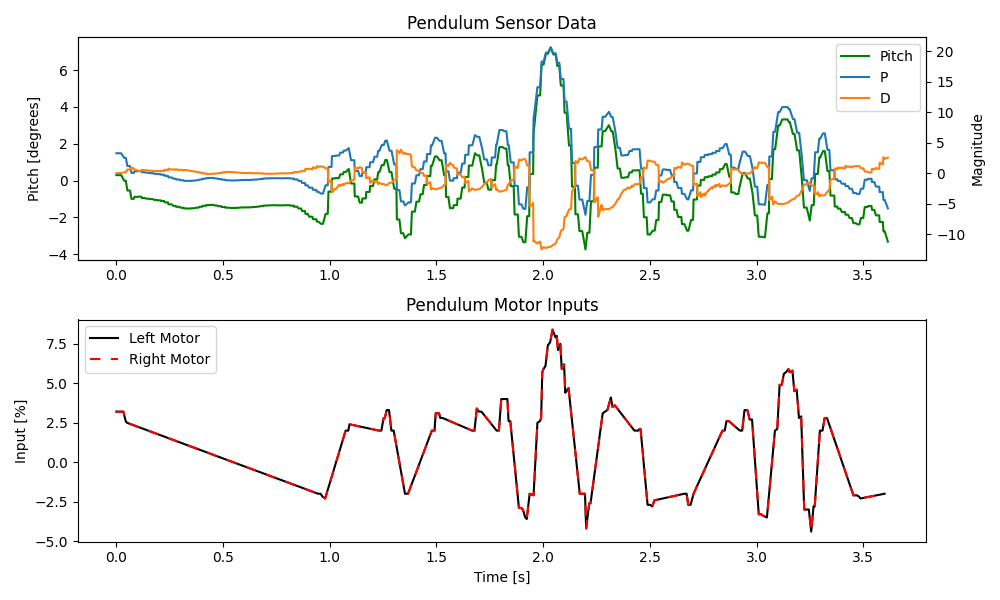
Next, I added support for a spin speed so that the car could turn on-axis while keeping itself upright. I figured that a bit of spin would help stabilize the system, plus it would look cool and demonstrate greater control over the robot. This next video shows an example.

My second spin test went better. I also recorded data for this one.

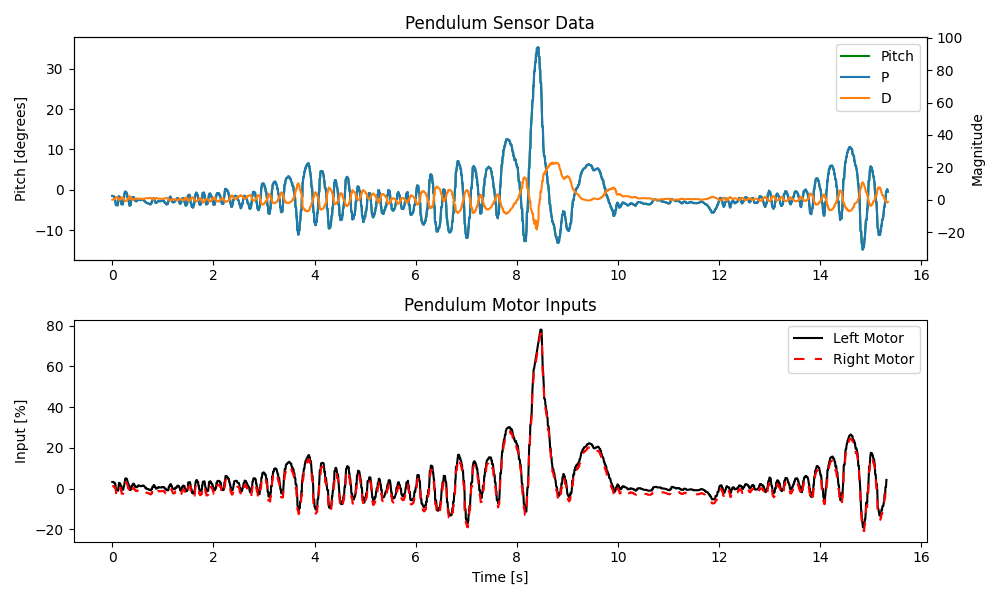
I then tried to increase the spin speed a little. It went okay for a bit before the car ran off on me.

And lastly, here's a test of considerably faster spin. It... didn't go well. That much spin was just too unstable.

All in all, the inverted pendulum control isn't perfect because the motors aren't terribly precise and the wheels aren't completely smooth and round, but it's pretty darn good and brings a huge smile to my face every time I play with it. Perhaps some long, thin extensions on the chassis could help stabilize the system, but I wanted to get as close with the car on its own as I could.

There are still some other ideas that could be applied to this. Had my motors been strong enough to perform a flip in Lab 8, I would tried to get the car to stand up and self-balance from a typical resting position, but alas, this was not within my reach. Maybe this effect could still be achieved by driving the car into a wall to induce a flip. I leave that as a reader's exercise.

Conclusion

This lab was an unexpectedly fun adventure. What started out as a friendly competition between Leo and me on ECE Robotics Day turned into a valuable exploration of complex dynamics. I only wish more students could have had the chance to pursue this challenge.

As this marks the end of Fast Robots for this year, I want to say a very warm thank you to Jonathan Jaramillo and the wonderful TAs who have all been so kind, helpful, and supportive throughout the semester. This was one of my favorite classes I've ever taken at Cornell, and I count myself lucky that I got to experience it with such awesome people!

Thank you and good bye!